关于两道动态规划的思考

说到动态规划，离不开一个爬楼梯的问题和一个铺砖快的问题。
爬楼梯的问题：

一个N层的楼梯，一次可以走一步或者两步，求走到楼梯顶部的所有步数

铺砖快的问题：

一个2*n的地方，需要铺上瓷砖，但是瓷砖的规格只有 2x1 的，求多少种铺法。

计算到顶层的最小问题：

On a staircase, the i-th step has some non-negative cost cost[i] assigned (0 indexed).
Once you pay the cost, you can either climb one or two steps. You need to find minimum cost to reach the top of the floor, and you can either start from the step with index 0, or the step with index 1.

也就是说，可以从0或者1开始选择起点，而且每一步都可以选择走一步还是两步。

走楼梯

首先这两道题目都可以使用递归来实现，关于爬楼梯的问题，一般是采用递归实现，如下：

  /**
     * 
     * @param step 表示从第几步开始走
     * @param end 表示有多少层楼梯
     * @return
     */
private static int  upLouti(int step ,int end){
        if(step == end || step == end -1 ){
            return 1;
        }
         return upLouti(step+1,end) + upLouti(step+2,end);
    }

那么此题的递归解法就是从0一直求到end，直到结束。

铺瓷砖

铺瓷砖也是类似的一个解法，也就是如果第一次是横着铺，那么下面一个肯定也是只能横着铺。如果第一个瓷砖是竖着铺的，那么可以直接进行长度减1，然后再计算。

第一次铺：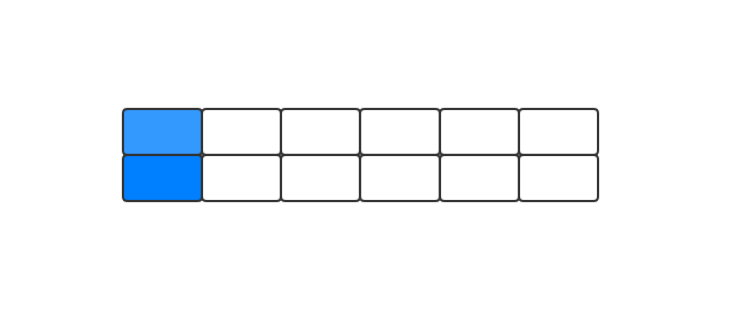

可以看到，如果第一次铺的砖块是竖着铺的话，那么剩余的计算就是n-1。

如果第一次是横着铺的话，那么其下面的一块砖肯定也是只能横着铺的，所以直接长度减2，计算就是n-2

代码如下：

private static int puCiZhuan(int step ,int end){
       if(step >= end){
           return 0;
       }
       if(step ==  end -1){
           return 1;
       }
       if(step == end -3){
           return 2;
       }
       return puCiZhuan(step+1,end)  + puCiZhuan(step + 3 ,end);
   }

最小路径到顶点

当在解决这个问题的时候，不能和走楼梯有一样的思路了，因为该题不仅仅需要考虑下一步的位置，还需要考虑下下一步的位置。
例如0,2,2,1，如果只考虑单步的话，那么它的最优解就是1+2 =3 ，但是其实着一道题目的最优解是2+0=2 ,所以在这里需要考虑的是如何保存上一次的结果然后进行比较。

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int f1 = 0, f2 = 0;
        for (int i = cost.length - 1; i >= 0; --i) {
            int f0 = cost[i] + Math.min(f1, f2);
            f2 = f1;
            f1 = f0;
        }
        return Math.min(f1, f2);
    }
}

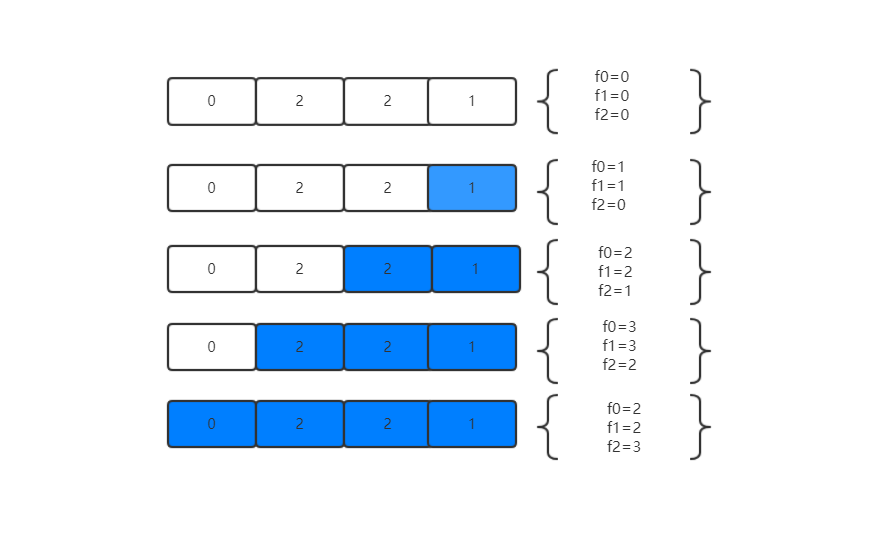
所以可以看到在该算法中，其中f2一直保存着上一次的计算结果